MIT18.06 Linear Algebra

前言

MIT 18.06 Linear Algebra 公开课，由Gilbert Strang教授主讲，b站视频地址，共35讲。

讲座内容

Lecture 1: The Geometry of Linear Equations

从线性方程组出发，逐步引出线性代数。

Lecture 2: Elimination with Matrices

介绍“消元法”求解线性方程组，引出逆矩阵。

Lecture 3: Multiplication and Inverse Matrices

1. 矩阵乘法\(A_{m\times n} B_{n\times p}=C_{m\times p}\)的5种表示：

   • \(C_{ij}=\sum_{k=1}^n A_{ik}B_{kj}\)
   • \(C\)的列向量是\(A\)的列向量的线性组合
   • \(C\)的行向量是\(B\)行向量的线性组合
   • sum of （ \(A\)的一列 \(\times\) \(B\)的一行 ）
   • 块矩阵乘法

2. 方阵的可逆性

   • 可逆 \(\Longleftrightarrow\) 非奇异（non-singular）

• 高斯-若尔当（Gauss-Jordan）消元
  • 消元矩阵E（elimination matrix）
  • 将矩阵\(A\)后边加上单位阵\(I\)一起做变换，将得到\(E [A\quad I] = [I\quad ?]\)，根据块矩阵乘法，\(EA=I\)
  • \((AB)^{-1}=B^{-1}A^{-1}\)

Lecture 4: Factorization into A = LU

1. \(AB,A^T\)的逆
2. 消元矩阵（elimination matrix）的乘积，以这种总的思路审视高斯消元
   • \(A=LU\), \(L:\) 下三角矩阵，\(U:\)上三角矩阵（先考虑在消元时，不需要row exchanges的情况，即不需要调整主元的位置，没有0在主元位置）
   • \(E_{32}E_{31}E_{21}A=U\)
     • \(A = E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}U\)
     • \(LU\)包含了\(A\)的所有信息，求解的复杂度在\(O(n^3)\)
   • 允许row exchanges，需要使用置换矩阵\(P\)（Permuations，将单位阵的行交换后得到）
     • \(P^{-1}=P^T\)
     • \(4\times 4\)的置换矩阵有24种

Lecture 5: Transposes, Permuations, Spaces \(\mathbb{R}^n\)

1. 置换矩阵
2. 转置
3. 向量空间，子空间
   • 零向量非常重要

Lecture 6: Column Spae and Nullspace

子空间的交集仍是子空间。

1. 列空间
   • \(A\)的列空间是\(A\)的所有列的线性组合，记作\(C(A)\)
   • \(Ax=b\)有解，当且仅当\(b\)在\(A\)的列空间中
2. 零空间
   • \(Ax=0\)的所有解

Lecture 7: Solving Ax=0 Pivot Variables, Special Solutions

介绍求解\(Ax=0\)的具体算法。

目标是零空间不会改变 ，在消元过程中，解是不会变的，所以零空间不会改变。

主元（pivot variables）的数量就是秩。

• \(Ax=0\)，在消元过程中，形成阶梯形式矩阵，判断主元（pivot variables）和自由变量（free variables），自由变量任意取值（001,100,010这样取值）确定特解（special solutions），特解的线性组合都是所有解
• 简化行阶梯形式（reduced row echelon form）
  • 主元的上下都是0
  • Matlab中的rref函数
  • 零空间 \([-F;I]\)

Lecture 8: Solving Ax=b Row Reduced Form \(R\)

求解\(Ax=b\)。

1. 增广矩阵\([A\quad b]\);

2. 探讨可解性（solvability）

   • 如果\(A\)各行的线性组合得到零行，那么\(b\)中的元素同样组合必然等于0
     • 言下之意是\(b\)对可解性有约束
   • 第一步，先求特解\(x_{particular}\)
     • 先设所有自由变量为0，求出一个特解
   • 第二步，求零空间nullspace
   • 第三步，完整解为：
     • \(x_{complete} = x_{particular} + x_{nullspace}\)

3. \(Ax=b\)解的情况与秩\(r\)有关，记简化行阶梯形式为\(R\)，\(F\)代表其中的自由变量对应的列

   • \(r=m=n\)
     • \(R=I\)
     • 1个解
   • \(r=n<m\)
     • \(R=[I;0]\)
     • 0或1个解
   • \(r=m<n\)
     • \(R=[I\quad F]\)（这样的表述不够准确，\(I\)和\(F\)实际上可能交叉出现）
     • 无穷多解
   • \(r<m,r<n\)
     • \(R=[I\quad F; 0\quad 0]\)
     • 要么无解，要么无穷多解

矩阵的秩决定了方程组解的数目。

Lecture 9: Independence, Basis, and Dimension

1. 线性无关性（Linear Independence）
   • \(c_1x_1 + \dots + c_nx_n\ne 0\) （\(c_i\)不全为0）
   • 如果零空间\(N(A)\)存在非零向量，那么各列线性相关
   • 关注不为0的线性组合
2. 生成一个空间（Spanning a space）
   • 由一组向量生成空间，意味着这个空间由这组向量的线性组合构成
   • 关注所有线性组合
3. “基”和“维数”（Basis and dimension）
   • 生成空间时，最关心这样的向量组：既能生成空间，本身又是线性无关的
     • 引出了“基”的概念
     • 向量的个数足够多但又不会太多
     • 关注一组线性无关的向量，并张成空间
   • 重要性质：对于给定空间，空间中任意基的基向量个数是相等的
   • 基向量的个数被称为维数
     • 对同一个空间来说，所有基的向量个数是一样的

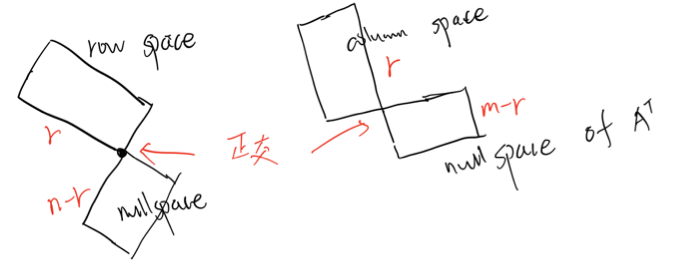
Lecture 10: The Four Fundamental Subspaces

介绍4个基本子空间，需要回答两个基本问题：

• “基”是什么
• “维数”是多少

1. 列空间\(C(A)\)

   • \(\mathbb{R}^m\)的子空间

   • \(dimC(A)=r\)

   • 基就是主列（pivot columns）

     • 注意，简化行阶梯形式\(R\), \(C(R)\ne C(A)\)
       • “行变换”不会对行空间有影响，行空间就是\(R\)的前\(r\)行

2. 零空间\(N(A)\)

   • \(\mathbb{R}^n\)的子空间
   • \(dimN(A)=n-r\)
   • 基就是\(Ax=0\)特解组成的矩阵（special solutions）

3. 行空间\(C(A^T)\)

   • \(\mathbb{R}^n\)的子空间

   • \(dimC(A^T)=r\)

   • 将\(A\)进行行变换得到\(R\)

     • “行变换”不会对行空间有影响，行空间就是\(R\)的前\(r\)行

4. \(A^T\)的零空间\(N(A^T)\)（也被称为左零空间）

   • \(\mathbb{R}^m\)的子空间
   • \(dimN(A^T)=m-r\)
   • 相当于\(A^Ty=0\Longrightarrow y^TA=0\)
     • 高斯-若尔当消元 \(E[A_{m\times x}\quad I_{m\times m}]\longrightarrow [R_{m\times n}\quad E_{m\times m}]\), 初等行变换
     • 通过\(E\)来求基，\(R\)中的最后几行为0的话，正好是\(y^TA\)，\(y\)中向量将\(A\)的行向量组合为0

Lecture 11 Matrix Spaces Rank 1 - Small World Graphs

介绍由矩阵构成的“向量空间”，（满足向量空间的8大定律的元素都可以构成向量空间）。

比如\(M\)空间是所有\(3\times 3\)的矩阵，它的子空间有：

• 对称阵\(_{3\times 3}\)
• 上三角矩阵\(_{3\times 3}\)

举一个来自微分方程的例子，\(\frac{d^2y}{dx^2}+y=0\)的所有解：

• 即\(y^{\prime\prime}+y=0\)
• 特解：\(y=\cos x,\sin x\) （特解还有其它的）
• 完整解：\(y=c_1\cos x + c_2 \sin x\)
• \(\cos x,\sin x\)就是一组基

回到矩阵上，矩阵的最为关键的数字就是秩（rank），比如：

• \[A = \begin{bmatrix} 1 & 4 & 5 \\ 2 & 8 & 10 \end{bmatrix}= \begin{bmatrix} 1 \\ 2 \end{bmatrix} \begin{bmatrix} 1 & 4 & 5 \end{bmatrix}= \vec{u}\vec{v}^T \]
• 秩为1 的矩阵就像“积木”，搭建任何矩阵
• 例1: 所有秩4矩阵不能构成子空间
• 例2: 将朋友关系建模为矩阵，“六度分离猜想”（number six degrees of seperation）

Lecture 12 Graphs,Networks,Incidence Matrices

主要介绍线性代数的应用：

• 表示图结构
• 关联矩阵（Incidence Matrices）
  • 表示电路图，从节点出来用\(-1\)表示，进入节点用\(1\)表示，其它用0，节点\(x\)表示电势，\(Ax\)可以看作是节点间的电势差。
  • 四个基本子空间对应了物理应用中的定律
  • 主列（线性无关）对应的子图是个树
  • 维度公式\(dim N(A^T)=m-r\)可以推出欧拉公式：
    • #nodes - #edges + #loops = 1
• 基尔霍夫电流定律（Kirchoff's Current Law, KCL）

Lecture 13 Quiz 1 Review

习题课。

Lecture 14 Orthogonal Vectors and Subspaces

向量的正交，子空间的正交，基的正交。

矩阵\(A\)的4个基本子空间：行空间(row space)，零空间(nullspace)，列空间(column space)，\(A^T\)的零空间，关系如下：

• 正交向量，若\(\vec{x}\)和\(\vec{y}\)正交，则\(\vec{x}^T\vec{y}=0\)。

• 零向量与任意向量都正交。

• 子空间\(S\)与子空间\(T\)正交的意思是：

  • \(S\)中的每个向量都和\(T\)中的每个向量正交
  • 两个正交的子空间的交集一定不会是非零向量

• nullspace and row space are orthogonal complements (正交补) in \(\mathbb{R}^n\)

  • 表示零空间包含所有垂直于行空间的向量

• 目前为止讨论了以及即将讨论以下内容：

  • 一，线性代数的基本定理
    • 四个基本子空间的关系
    • 维数
  • 二，正交性
  • 三，基（正交基）

• 本章核心内容

  • \(Ax=b\)无解时怎么求？(下一章具体介绍)
    • 无解意味着\(b\)不在\(A\)的列空间中
    • 当\(A\)矩阵，\(m > n\)时，右侧取值大部分情况都无解，（消元后，A的最后几行是0，对b的约束更多）
    • \(A^TA\)矩阵
      • 因为\(Ax=0 \Longrightarrow A^TAx=0\)，所以\(N(A^TA)=N(A)\)
      • 当且仅当\(A\)的零空间只有零向量时，\(A^TA\)是可逆的
        • \(N(A)=0 \Longrightarrow N(A^TA)=0 \Longrightarrow N(A^TA)=n-r=0 \Longrightarrow A^TA\)的秩为\(n\)

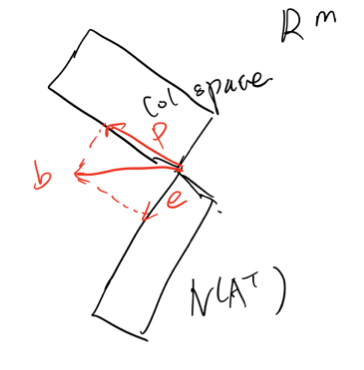
Lecture 15 Projections onto Subspaces

这一章主要介绍投影（Projection）和最小二乘法（Least Squares）。

• 投影矩阵

  

  • 把\(b\)投影到\(a\)上，记\(a\)上离\(b\)最近的点为\(p\)
    • \(p=xa\) (倍数)
    • \(a^T(b-xa)=0\)
    • \(x=\frac{a^Tb}{a^Ta}\)
    • \(p=a\frac{a^Tb}{a^Ta}\)
    • 记\(p=Pb\)，那么\(P=\frac{aa^T}{a^Ta}\)，\(P\)称为投影矩阵（projection matrix）
      • \(aa^T\)秩为1
  • 投影矩阵的2个性质
    • 对称：\(P^T=P\)
    • 如果投影2次，结果和1次一样：\(P^2=P\)
  • 推广到高维情况
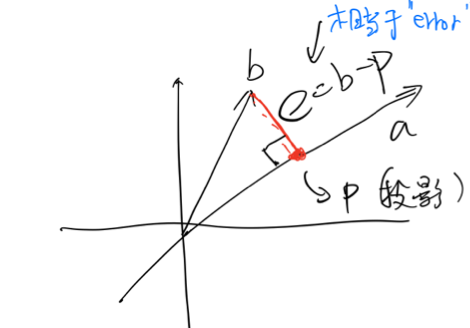
    • 动机，为什么要投影？
      • \(Ax=b\)也许无解，只能求解最接近的那个可解问题
        • \(Ax\)总是在\(A\)的列空间中，\(b\)不一定在（比如方程有噪声）
        • 微调\(b\)，把\(b\)变成列空间中最接近它的那一个
        • 将原问题换作求解\(A\hat{x}=p\)（有解的），\(p\)是\(b\)在列空间上的投影
          • \(\hat{x}\)不是原来的解，但是是最接近解的
    • \(b\)有两种情况
      • 一是在列空间中，那么投影就是它自己，投影后不改变原始解
      • 二是不在列空间中，原始方程无解，误差向量\(e=b-p\)，\(e\)垂直于超平面
    • 假设\(A=[a_1 \quad a_2]\)
      • \(p=A\hat{x}\)，找到\(\hat{x}\)
      • 关键在于\(e=b-p=b-A\hat{x}\)垂直于平面，得：
        • \(a_1^T(b-A\hat{x})=0,a_2^T(b-A\hat{x})=0 \Longrightarrow\)
        • \(A^T(b-A\hat{x})=0\)
        • 从上式可得，\(e\)在\(N(A^T)\)中，而\(N(A^T)\)与\(A\)的列空间\(C(A)\)是正交的，可得 \(e\perp C(A)\)
        • 从上面式子可得，非常重要的式子： \[A^TA\hat{x}=A^Tb\]
        • 关于上面这个式子的三个问题：
          • \(\hat{x}\)是什么
            • \(\hat{x}=(A^TA)^{-1}A^Tb\)
          • 投影是什么
            • \(p=A\hat{x}=A(A^TA)^{-1}A^Tb\)
          • 投影矩阵是什么
            • \(P=A(A^TA)^{-1}A^T\) (需要注意的是，括号不能随便打开，因为\(A\)不一定可逆)
            • 满足两个性质：
              • 对称
              • \(P^2=P\)
    • 应用（最小二乘法）

Lecture 16 Projection Matrices and Least Squares

投影、最小二乘法和最佳拟合曲线。

• 回顾投影矩阵

  

  • \(P=A(A^TA)^{-1} A^T\)
  • \(e=b-p=b-Pb=(I-P)b\)
    • 所以\(I-P\)是把\(b\)投影到\(N(A^T)\)上的投影矩阵

• 最小二乘法例子

  • 用\(y=C+Dt\)拟合3个点\((1,1),(2,2),(3,2)\)
  • 从投影矩阵角度考虑
    • \(A^TA\hat{x}=A^Tb\)
    • 求解\(\hat{x}\)
  • 从最小化均方误差
    • Minimize \(||Ax-b||^2=||e||^2\)
    • 微分方程求偏导
  • 二者最后得到的正规方程组相同

• 以上推导一直假设\(A^TA\)是可逆的，下面证明当\(A\)各列线性无关时，\(A^TA\)一定可逆：

  • \(A^TA\)要可逆的话，\(N(A^TA)\)一定只有零向量，即\(A^TAx=0\)只有零解，
  • 根据\(A^TAx=0\)，那么有\(x^TA^TAx=0\)，那么有\((Ax)^T(Ax)=0\)，（\(a^Ta\)是长度）,
  • 那么\(Ax\)一定是零向量，
  • 利用假设，\(A\)各列线性无关，可推出\(x=0\)

• 互相垂直的各列一定线性无关

  • 互相垂直的单位向量被称为标准正交向量组（orthonormal vectors）

Lecture 17 Orthogonal Matrices and Gram Schmidt

关于正交性的最后一讲，标准正交基，正交阵（orthogonal matrices），Gram-Schmidt方法。

• 当\(Q\)是方阵时，才称为正交矩阵
  • \(q_i,q_j\)表示标准正交向量
  • \(Q^TQ=I\)，\(Q^T=Q^{-1}\)
  • 比如置换矩阵（permutation matrix）
• \(Q\)是有标准正交向量的矩阵
  • 投影矩阵为\(P=Q(Q^TQ)^{-1}Q^T=QQ^T\)
  • 满足投影矩阵的2个性质
    • 对称性
    • \(Q^2=Q\)
  • 正规方程\(A^TA\hat{x}=A^Tb\)，对于正交矩阵来说，即\(Q^TQ\hat{x}=Q^Tb\)
    • \(\hat{x}=Q^Tb\)
      • \(\hat{x}_i=q_i^{T}b\)
• Gram-Schmidt 格拉姆-施密特正交化法
  • 对于线性无关的向量\(a,b\)
  • 第一步，求出正交向量组\(A,B\)
    • \(A=a\)
    • \(B=b-p=b-\frac{A^Tb}{A^TA}A\) ( 减去\(b\)在\(a\)上的投影)
  • 第二步，标准化\(q_1=\frac{A}{||A||},q_2=\frac{B}{||B||}\)
  • 泛化到3个向量\(a,b,c\)
  • 第一步，求正交向量组\(A,B,C\)
    • \(A=a\)
    • \(B=b-\frac{A^Tb}{A^TA}A\)
    • \(C=c-\frac{A^Tc}{A^TA}A - \frac{B^Tc}{B^TB}B\)
• 换个角度看Gram-Schmidt正交化方法
  • 以前的消元法相当于\(A=LU\)
  • Gram-Schmidt相当于\(A=QR\)
    • \(R\)是上三角矩阵，因为后面构造的\(q\)向量垂直于先前的向量
• 总结
  • \(A\)的各列线性无关，Gram-Schmidt构造一组标准正交列的矩阵\(Q\)
    • \(A\)和\(Q\)通过上三角矩阵\(R\)联系：\(A=QR\)

Lecture 18 Properties of Determinants

方阵的行列式及其10条性质，由1，2，3条性质可推其它。

1. 单位阵行列式为1，\(\det I = 1\) 。
2. 交换行会使行列式正负号相反。
   • 由1，2可得置换矩阵的行列式。
3. 对于某一行，线性（Linear for each row）
   • (a): \[\begin{vmatrix} t\cdot a & t\cdot b \\ c & d \end{vmatrix}=t\begin{vmatrix} a & b \\ c & d \end{vmatrix}\]
   • (b): \[\begin{vmatrix} a+a^{\prime} & b+b^{\prime} \\ c & d \end{vmatrix}=\begin{vmatrix} a & b \\ c & d \end{vmatrix} + \begin{vmatrix} a^{\prime} & b^{\prime} \\ c & d \end{vmatrix}\]
4. 两行相等会使行列式为0。
   • 用性质2可证，交换两行，符号交换但相等
5. 从行\(k\)减去行\(i\)的\(l\)倍，行列式不变
   • \[\begin{aligned}\begin{vmatrix} a & b \\ c-la & d-lb \end{vmatrix} &\overset{性质3}{=} \begin{vmatrix} a & b \\ c & d \end{vmatrix} + \begin{vmatrix} a & b \\ -la & -lb \end{vmatrix}\\ &\overset{性质3}{=} \begin{vmatrix} a & b \\ c & d \end{vmatrix} - l \begin{vmatrix} a & b \\ a & b \end{vmatrix} \\ &\overset{性质4}{=} \begin{vmatrix} a & b \\ c & d \end{vmatrix} - 0 \end{aligned} \]
6. 若有一行为0，则\(\det A = 0\).
7. 上三角矩阵\(u\)
   • \[\det u = \begin{vmatrix} d_1 & ... & ... \\ 0 & \ddots & ... \\ 0 & 0 & d_n\end{vmatrix}=d_1 \cdot d_2\cdot \cdots d_n\]
8. 当且仅当\(A\)是奇异（singular）的，行列式为0.
   • 求行列式方法，先求上三角，再求对角，（和消元法一样）
9. \(\det AB = (\det A)(\det B)\)
   • \(\det A^{-1} = \frac{1}{\det A}\)
   • \(\det A^2 = (\det A)^2\)
   • \(\det 2A = 2^n \det A\)
10. \(\det A^T = \det A\)

Lecture 19 Determinant Formulas and Cofactors

介绍求\(\det A\)的公式，代数余子式(Cofactor formula)，Tridiagonal matrices（除三条对角线上，其它为0）。

利用行列式的基本性质1-3，可以将原行列式化为各行各列仅有一个元素的方阵的行列式之和。

Big Formula:

• \[\det A = \sum_{n!} \pm a_{1\alpha}a_{2\beta}a_{3\gamma}\cdots a_{n\omega} \]，其中\((\alpha, \beta, \gamma, \dots,\omega)\)是\((1,\dots,n)\)的一个排列，正负号待定。

代数余子式（cofactors）：

• 作用是把n阶行列式化简为n-1阶行列式。
• cofactor of \(a_{ij}=C_{ij}=\pm\) 把第\(i\)行和第\(j\)列去掉的\(n-1\)阶矩阵，
  • \(i+j\)为偶，符号为正
  • \(i+j\)为奇，符号为负
• \(\det A = a_{11}C_{11} + a_{12}C_{12} + \cdots + a_{1n}C_{1n}\)

Lecture 20 Cramer's Rule, Inverse Matrix, and Volume

关于行列式的最后一课，行列式的应用。

• 逆矩阵\(A^{-1} = \frac{1}{\det A} C^T\)
  • \(C\)是由代数余子式组成的矩阵，\(C^T\)一般称作伴随矩阵
• 克莱姆法则 （Carmer's Rule）
  • \(x=A^{-1}=\frac{1}{\det A}C^T b\)
  • \(x_1=\frac{\det B_1}{\det A},x_2=\frac{\det B_2}{\det A},\dots\)
    • \(B_i\)是将\(A\)中的第\(i\)列用\(b\)替代而得到的矩阵。
  • 克莱姆法则一般不用来解方程，计算太复杂，Matlab中用消元法解方程。
• 行列式的应用
  • 行列式的绝对值等于一个箱子的体积，正负号表示左手系还是右手系。
  • 如果三角形的顶点不在原点，三个顶点坐标为\((x_1,y_1),(x_2,y_2),(x_3,y_3)\)，面积为：
    • \[\begin{vmatrix} x_1 & y_1 & 1 \\ x_2 &y_2 &1 \\ x_3 &y_3 & 1 \end{vmatrix}\]
    • 具体推导过程，对上面的矩阵消元，想当于使三角形回到原点

Lecture 21 Eigenvalues and Eigenvectors

方阵特征值和特征向量。

• 特征向量
  • \(Ax\)平行于\(x\)的特征向量
    • \(Ax=\lambda x\)
    • 如果\(A\)是奇异的（可以把非零向量变成0），\(\lambda=0\)是特征值。
• 先看投影矩阵\(P\)
  • 任何平面上的向量就是特征向量，\(\lambda=1\)，因为\(Px=x\)
  • 任何垂直于平面的向量，\(\lambda =0\)，因为\(Px=0\)
• 性质
  • 特征值的和是矩阵\(A\)的对角线元素之和(\(a_{11}+a_{22}+\dots+a_{nn}\))
• 如何求解特征值
  • 重写为\((A-\lambda I)x=0\)，\(\lambda\)未知，\(x\)未知
    • 除了零向量，要有非零\(x\)的话，\(A-\lambda I\)必须是奇异的 \(\Longrightarrow\) \(\det(A-\lambda I)=0\)
    • 称为“特征方程（characteristic equation）”or 特征值方程“eigenvalue equation”
    • \(\lambda\)值可能重复
• if \(Ax=\lambda x\), then \((A+3I)x=Ax+3x=\lambda x+ 3x = (\lambda + 3)x\)
  • 特征值加3，特征向量不变
• 旋转矩阵会有复数解
  • 反对称矩阵会出现复数解

Lecture 22 Diagonalizing a matrix and Powers of A

特征值的第二讲。

• 对角化一个矩阵：\(S^{-1}AS=\Lambda\)，
  • \(S\)由\(A\)的特征向量组成
    • 可逆\(\Longrightarrow\)\(n\)个线性无关的特征向量
  • 假设\(A\)有\(n\)个线性无关的向量，把它们作为\(S\)的列向量可得：
    • \[\begin{aligned} AS &= A[x_1 \quad x_2 \dots x_n]\\ &=[\lambda_1 x_1\quad \dots \lambda_n x_n ] \\ &=[x_1\dots x_n] \begin{bmatrix} \lambda_1 \dots 0 \\ 0 \dots \lambda_n \end{bmatrix} \\ &=S\Lambda \end{aligned}\]
    • \(\Lambda\)是对角矩阵：特征值矩阵
  • 特征值和特征向量提供了理解矩阵幂的一种好方法
    • 假设\(Ax=\lambda x\)，有\(A^2x=\lambda Ax=\lambda^2x\)
    • \(A^2=S\Lambda S^{-1}S\Lambda S^{-1}=S\Lambda^2S^{-1}\)
    • \(A^k=S\Lambda^kS^{-1}\)
  • 定理
    • 如果所有\(|\lambda_i|<1\)，那么当\(k\rightarrow \infty\)时，\(A^k\rightarrow 0\)
    • 以上这些推导的前提条件是\(n\)个线性无关的特征向量
  • 哪些矩阵可对角化呢？
    • 如果\(A\)矩阵的所有特征值\(\lambda\)是不同的（没有重根），那么\(A\)肯定有\(n\)个线性无关的特征向量。
      • 充分但不必要
    • 如果\(A\)的特征值有重复，A可能有，也可能没有 \(n\)个线性无关的特征向量。
• Powers of A
  • \(\mu_{k+1}=A\mu_k\)
  • 一阶差分方程\(\mu_{k+1}=A\mu_k\)，给定起始值\(\mu_0\)。求解：
    • 把\(\mu_0\)写成特征向量的线性组合后再处理
      • \(\mu_0=c_1x_1 + c_2x_2 + \dots + c_n x_n\)
      • \(\begin{aligned} A^{100}\mu_0 &= c_1\lambda_1^{100}x_1 + c_2\lambda_2^{100}x_2 + \dots + c_n\lambda_n^{100}x_n \\ &=S \Lambda^{100} c \end{aligned}\)
    • 斐波那契数列例子
      • \(0,1,1,2,3,4,8,13,\dots,F_{100},\dots\)
      • 不禁要问
        • 这个数列的“增长速度如何”？
          • 增长速度由特征值决定
      • \(F_{k+2}=F_{k+1}+F_k\)，二阶差分方程
        • 写成一阶：\[\mu_k = \begin{bmatrix} F_{k+1} \\ F_k \end{bmatrix}\]
        • 方程组为：
          • \[\begin{cases} F_{k+2} = F_{k+1} + F_k \\ F_{k+1} = F_{k+1} \end{cases}\]
        • 可得
          • \[\begin{aligned} \mu_{k+1} &= \begin{bmatrix} 1 & 1 \\ 1 & 0\end{bmatrix} \mu_k \\ &= \begin{bmatrix} 1 & 1 \\ 1 & 0\end{bmatrix} \begin{bmatrix} F_{k+1} \\ F_k\end{bmatrix} \end{aligned}\]
          • 系数矩阵是对称阵，可知
            • 特征值是实数
            • 特征向量一定正交
          • 求系数矩阵的特征值和特征向量
            • \(\det(A-\lambda I)=0\Longrightarrow \lambda_1=\frac{1+\sqrt{5}}{2},\lambda_2=\frac{1-\sqrt{5}}{2}\)
            • 特征向量：\[x_1=\begin{bmatrix}\lambda_1 \\ 1 \end{bmatrix}, x_2=\begin{bmatrix}\lambda_2 \\ 1 \end{bmatrix}\]
          • 然后把\[\mu_0 = \begin{bmatrix}F_1 \\ F_0 \end{bmatrix}=c_1x_1 + c_2x_2\]
            • \(c_1 = \frac{1}{\sqrt{5}},c_2=-\frac{1}{\sqrt{5}}\)
        • 特征值决定增长的趋势，发散至无穷还是收敛于0

Lecture 23 Differential Equations and exp(At)

微分方程\(\frac{du}{dt}=Au\)和矩阵的指数\(e^{At}\)。

• 微分方程
  • 例子
    • \(u(0)=[1\quad0]^T\)
    • \(\frac{du_1}{dt}=-u_1 + 2u_2\)
    • \(\frac{du_2}{dt}=u_1-2u_2\)
    • 系数矩阵\(A=\begin{bmatrix} -1 & 2 \\ 1 & -2 \end{bmatrix}\)
      • 奇异的
      • \(\lambda=0,-3\)
      • \(x_1=\begin{bmatrix}2 \\ 1 \end{bmatrix},x_2=\begin{bmatrix}1 \\ -1 \end{bmatrix}\)
    • 解的形式是$u_t=c_1e^{_1t}x_1 + c_2e^{_2t}x_2 $
    • 首先根据\(u_0\)确定\(c_1=\frac{1}{3},c_2=\frac{1}{3}\)
    • 然后得到\(u(t)=\frac{1}{3}\begin{bmatrix}2 \\ 1\end{bmatrix} + \frac{1}{3}e^{-3t}\begin{bmatrix} 1 \\ -1\end{bmatrix}\)
    • 可以看出稳态是\(u(\infty)=\begin{bmatrix} 2 \\ 1 \end{bmatrix}\)
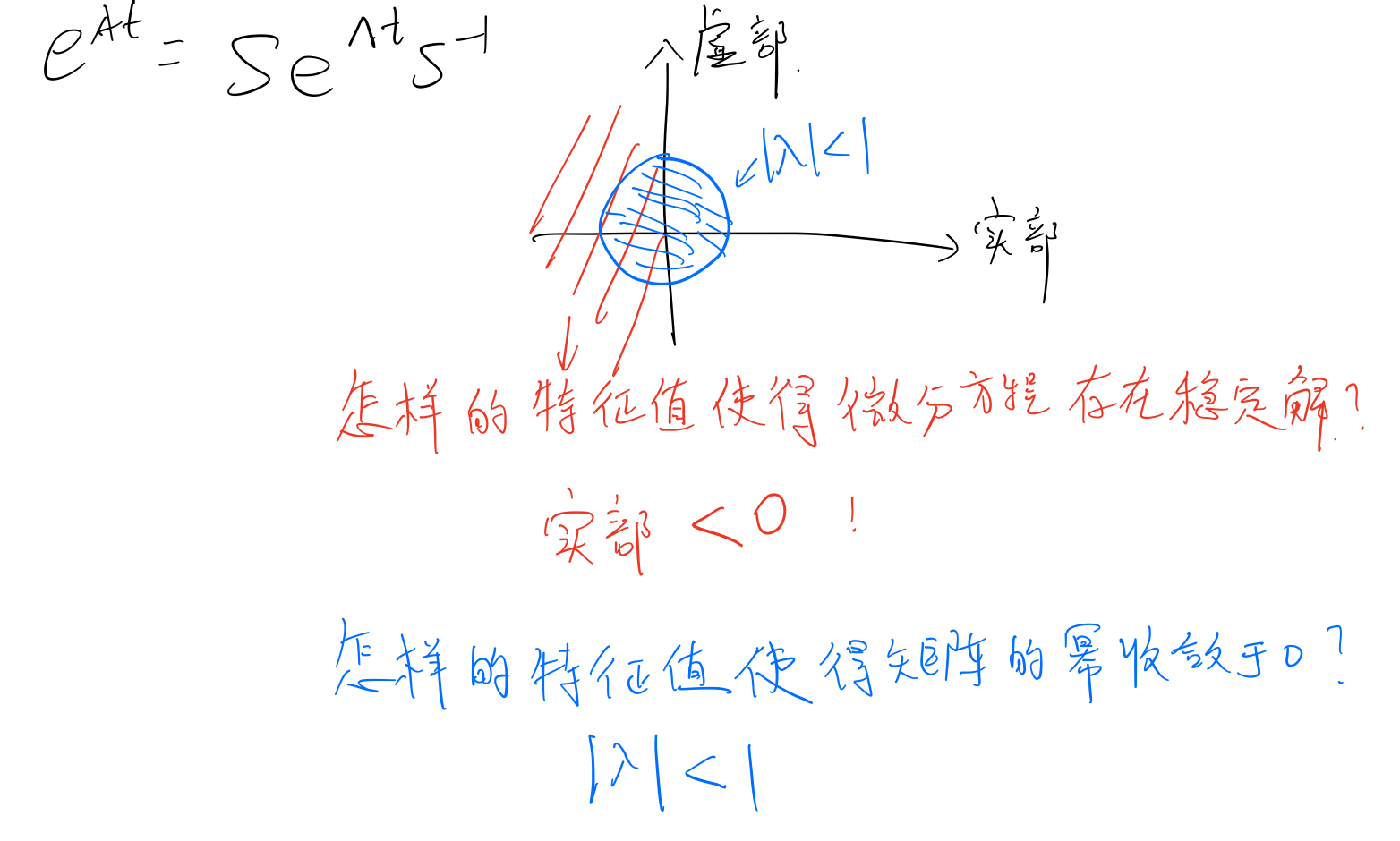
    • 什么情况下才有稳态？
      • 1. 稳定性 stability，需要\(e^{\lambda t}\rightarrow 0\)，即\(Re \lambda<0\) （\(Re\lambda\)表示\(\lambda\)的实数部分）
      • 2. steady state需要\(\lambda_1=0,\)其它\(Re\lambda<0\)
      • 3. 无法收钱，if 任一\(Re\lambda > 0\)
    • \(2\times 2\)矩阵的有稳态的条件是
      • trace \(\lambda_1 + \lambda_2<0\)
      • \(\det=\lambda_1 \cdot \lambda_2 > 0\)
    • 回到原来的方程组\(\frac{du}{dt}=Au\)
      • 矩阵\(A\)表明\(u_1,u_2\)耦合，关键是特征向量如何解耦。
      • 设\(u = Sv\)，\(S\)由特征向量组成，
      • \(S\frac{dv}{dt}=ASv\Longrightarrow \frac{dv}{dt}=S^{-1}ASv=\Lambda v\)
        • 关键在于以特征向量为基，将\(u\)表示为\(Sv\)
        • \(\Longrightarrow v(t)=e^{\Lambda t}v(0)\)
        • \(u(t)=Se^{\Lambda t} S^{-1}u(0)=e^{At}u(0)\)
      • 矩阵指数（Matrix exponentials）
        • \(e^{At}=I+At+\frac{(At)^2}{2}+\frac{(At)^3}{6}+\dots+\frac{(At)^n}{n!}+\dots\)
          • 类似于\(e^x=\sum_{0}^{\infty}\frac{x^n}{n!}\)
        • \((I-At)^{-1}=I+At+(At)^2+(At)^3+\dots\)
          • 要求\(At\)的特征值都小于1
          • 类似于\(\frac{1}{1-x}=\sum_{0}^{\infty} x^n\)
        • 证明\(e^{At}\)等于\(Se^{\Lambda t}S^{-1}\)
          • \(\begin{aligned} e^{At}&=I+At+\frac{(At)^2}{2}+\dots+\frac{(At)^n}{n!}+\dots \\ &=I+S\Lambda S^{-1}t+ \frac{S\Lambda^2 S^{-1}t^2}{2} + \dots \\ &=SS^{-1} + S\Lambda S^{-1}t+\frac{S\Lambda^2 S^{-1}t^2}{2}+\dots \\ &= Se^{\Lambda t}S^{-1} \end{aligned}\)
        • \[e^{\Lambda t}= \begin{bmatrix} e^{\lambda_1 t} & \dots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \dots & e^{\lambda_n t} \end{bmatrix}\]
          • 如果所有特征值的实部为负（\(Re\lambda_i < 0\)），对角线的指数收敛于0。
      • 
      • 只有1个方程：\(y^{\prime\prime}+by^{\prime}+ky=0\)，二阶微分方程
        • 把1个二阶微分方程化为一阶方程组
        • 令\(u=\begin{bmatrix}y^{\prime} \\ y \end{bmatrix}\),
        • \[u^{\prime}=\begin{bmatrix}y^{\prime\prime} \\ y^{\prime} \end{bmatrix}=\begin{bmatrix}-b & -k \\ 1 & 0\end{bmatrix}\begin{bmatrix}y^{\prime} \\ y\end{bmatrix}\]
        • 同理五阶的微分方程也可以化为一阶方程组，对应矩阵为：
          • \[\begin{bmatrix}\dots & \dots & \dots & \dots & \dots \\ 1 & & & & \\ & 1 & & & \\ & & 1 & & \\ & & & 1 & 0 \end{bmatrix}\]

Lecture 24 Markov Matrices, Fourier Series

主要内容包括：马尔可夫矩阵和它的稳态，Fourier Series Projections，特征值的应用。

• Markov Matrices （马尔可夫矩阵）
  • \[\begin{bmatrix} .1 & .01 &.3 \\ .2 &.99 &.3 \\ .7 &0 &.4 \end{bmatrix}\]
  • 满足以下条件:
    • 所有元素\(\ge 0\)
    • 每一列加起来为1 \(\Longrightarrow \lambda=1\)是特征值
    • 它的幂也是马尔可夫矩阵
  • 稳态和特征值1及其特征向量关联在一起
  • 稳态的关键在于
    • \(\lambda=1\)是特征值
    • 所有其它特征值\(|\lambda_i|<1\)
    • \(\mu_k=A^k\mu_0=c_1\lambda_1^kx_1+c_2\lambda_2^k+\dots\)， 当满足上面两个条件时，这个式子趋近于\(c_1x_1\)
  • 证明：每一列的和为1，那么1是特征值
    • 思路：如果\(A-1\cdot I\)是奇异的，那么1是特征值
    • 由于\(A-1 \cdot I\)每一列和为0，相当于要证：每一列和为0时，矩阵是奇异的
    • 方法
      • 1. 求行列式\(\rightarrow\) 太复杂
        2. 奇异的，意味着
           1. 列向量线性相关
           2. 行向量线性相关（正好有\(1\cdot row_1 + 1 * row_2 + ...=0\)）
    • 以3阶矩阵为例，说明\((1,1,1)\)在\(n(A^T)\)（转置的零空间，左零空间）中
      • then，\(x_1\)（\(\lambda=1\)对应的特征向量）在\(n(A-I)\)中
    • \(A\)和\(A^T\)的特征值是一样的
      • \(\det(A-\lambda I)=0\)
      • 利用\(\det(A)=\det(A^T)\)
      • $(A-I)=0 $
      • $(A-I)^T =0 $
      • \(\det(A^T-\lambda I)=0\)
  • 应用，马尔科夫矩阵，
    • 两个地方的人口迁移问题
• 傅立叶级数
  • 回归带有标准正交基的投影问题
    • 标准正交基：\(q_1,\dots,q_n\)
    • \(v=x_1q_1+x_2q_2+\dots+x_nq_n\)
    • 基向量的系数很容易求出：\(q_1^Tv=x_1q_1^Tq_1+0+\dots+0=x_1\cdot 1\)
  • Fourier series可以把任何周期函数或周期信号分解成一个（可能由无穷个元素组成的）简单振荡函数的集合（PERIODIC Function，周期函数）
  • 已知函数\(f(x)=a_0\cdot 1 +a_1\cos x+b_1\sin x+a_2\cos 2x + b_2\sin 2x + \dots\)
    • 无穷维，关键性质是正交
    • “正交”
      • 向量的正交是\(y^Tx=0\)
      • 函数的正交（对于函数\(f,g\)）是\(f^Tg=\int_0^{2\pi}f(x)g(x)=0\)
    • 怎么计算\(a_1\)
      • \(\int_{0}^{2\pi}f(x)\cos xdx=0 + a_1\int_{0}^{2\pi}(\cos x)^2dx + 0 + \dots\)

Lecture 25 Review for Quiz 2

习题课，包括以下内容：

• 投影，最小二乘，Gram-Schmidt正交化
• 行列式的性质，代数余子式
• 特征值，对角化，矩阵的幂

Lecture 26 Symmetric Matrices and Positive Definiteness

本讲是关于对称矩阵的知识，\(A=A^T\)，意味着：特征值是实数，特征向量互相垂直

• 根据矩阵的对角化：\(A=S\Lambda S^{-1}\)，\(S\)由特征向量构成，\(\Lambda\)由特征值构成
  • 对称矩阵\(A=Q\Lambda Q^{-1}=Q\Lambda Q^{T}\)，\(Q\)是标准正交向量
  • 为什么对称阵的特征值是实数？
    • 先回归共轭：\(\overline{a+ib}=a-ib\)
    • \(Ax=\lambda x\) （1.）总可以得到\(\bar{A}\bar{x}=\bar{\lambda}\bar{x}\) （2.）
      • \(A\)为实矩阵时
        • \(\bar{A}=A\)
        • 转置2. 可得\(\bar{x}A^T = \bar{x}^T \bar{\lambda}\)
        • 由于对称，\(\bar{x}A = \bar{x}^T\bar{\lambda}\) (3.)
        • 1.左乘\(\bar{x}^T\)，\(\bar{x}^TAx = \lambda \bar{x}^Tx\)
        • 3.右乘\(x\),，\(\bar{x}^TAx = \bar{x}^T\bar{\lambda}x\)
        • 由上面两个式子可得，\(\lambda \bar{x}^Tx=\bar{\lambda}\bar{x}^Tx\Longrightarrow \lambda =\bar{\lambda}\), 所以\(\lambda\)是实数
      • A为复矩阵时
        • 转置2.可得，\(\bar{x}^T\bar{A}^T = \bar{x}^T \bar{\lambda}\) (4.)
        • 1.左乘\(\bar{x}^T\)，\(\bar{x}^TAx = \lambda \bar{x}^Tx\)
        • 4.右乘\(x\),，\(\bar{x}^T\bar{A}^Tx = \bar{x}^T\bar{\lambda}x\)
        • 所以，当且仅当\(A=\bar{A}^T\)时，才有\(\lambda\)是实数
        • 定义新的符号：\(A^H \triangleq \bar{A}^T\)，表示共轭转置
  • 对称阵可以分解为\(A=Q\Lambda Q^T=\lambda_1q_1q_1^T+\lambda_2q_2q_2^T+\dots\)
    • \(q_iq_i^T\)是投影矩阵
    • 每个对称阵都是一些互相垂直的投影矩阵的组合，（理解谱定理的另一种方法）
  • 上面知道了对称阵的特征值是实数了，下面分析一下特征值的正负
    • 对于对称阵来说，主元的符号与特征值的符号相同
      • 正主元的个数等于正特征值的个数
    • 什么是正定矩阵（positive definite matrix）（对称的）
      • 所有的特征值是正的
      • 所有的主元是正的
      • 所有的子行列式是正的（从左上角开始，\(1\times1,2\times 2...\), 即顺序主子式都大于0）
      • 微分方程需要根据特征值的正负判断稳定性